The terms alternating & direct current are frequently used in the field of electronics. So, an alternating waveform is one that is related to alternating current.

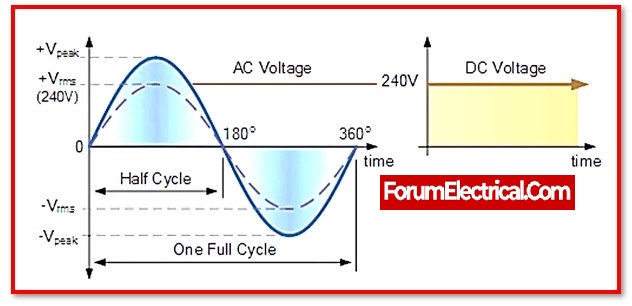
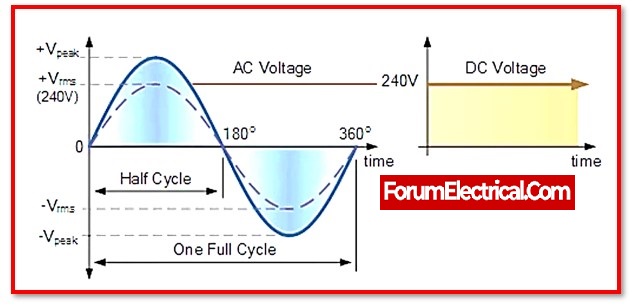
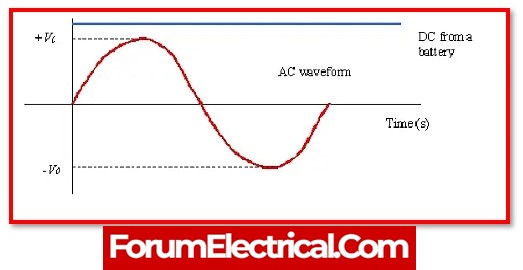
This means it is a periodic waveform that alternates between negative & positive values. A sinusoidal waveform is the most general type of the waveform used to represent this.

When it comes to the direct current waveform, the current & voltage values are essentially stable. It is extremely simple to represent stable values & their magnitude values.

The magnitude values of the AC waveforms are not as simple as they appear because they vary continuously with time. There are numerous methods for determining this, but “RMS Voltage” among the most popular.

What is meant by RMS Voltage?

RMS –Root Mean Square

The square root of the mean square of the voltage signal’s instantaneous values is known as an RMS voltage.

The quadratic mean is other name for the RMS. In terms of an integral (integration) of the squares of the instantaneous values over a cycle, RMS voltage may also be expressed for a continuously fluctuating voltage.

When functioning with an AC signal, the RMS value is very necessary, because an AC signal’s instantaneous value constantly fluctuates with respect to time. in contrast to a DC signal, which is often continuous.

Hence, it is not possible to do the computation using the voltage’s immediate value.

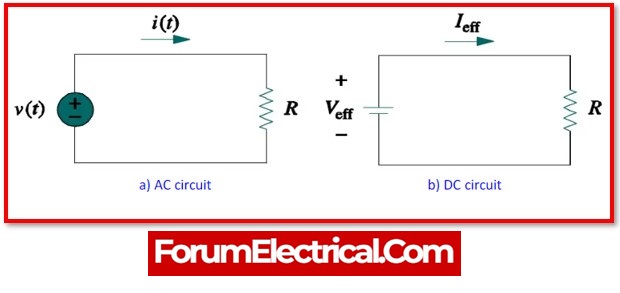
Since the RMS value provides the amount of AC power taken by a resistor that is comparable to the power pulled by a DC source, the RMS voltage is also called as the equivalent DC voltage.

It is known as √  of the average value of the double function of instantly created values.

V_RMS is the voltage value, while I_RMS is the RMS current value.

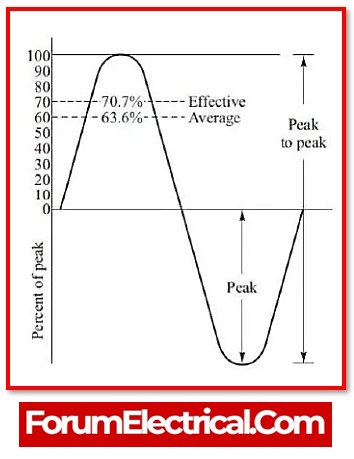
Effective Value of RMS Voltage

RMS values are determined exclusively for time-varying sinusoidal voltage (or) current values, where the magnitude of the wave changes with time, but not for DC waveform values, where the magnitude remains constant.

When the RMS value of an AC sine wave is compared to the RMS value of a comparable DC circuit that provides the same amount of electrical power with the same load, the value is known as the effective value.

I_eff represents the effective current value, while V_eff represents the effective voltage value. Instead, the effective value is also expressed as how many amperes (or) volts for a DC wave are comparable to related to the capacity to create a comparable amount of power.

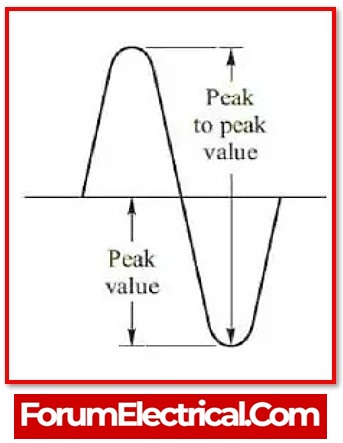
Peak Voltage

The peak voltage of a source is the greatest voltage it is capable of or will reach at its peak. The peak voltage, denoted by V_peak, is determined by tracing a line from the horizontal axis (at the 0-reference height) to the crest of the waveform.

RMS Voltage equation

It is more necessary to understand the RMS Voltage equation since it is used to compute a variety of values, and the fundamental equation is

V_RMS = V_peak-voltage X (1/ (√2)) = V_peak-voltage X 0.7071

The RMS voltage value is based on the magnitude of the alternating current waveforms and is not affected by the phase angle (or) frequency of the AC (alternating current) waveforms.

The resulting value is almost same in both the

1. Graphical methods and
2. Analytical methods.

This only occurs with sinusoidal waves. In the case of non-sinusoidal waves, the graphical method is the sole alternative. Instead of utilising the peak voltage, calculate the voltage that lies between two peak values, which is V_P-P.

The Sinusoidal RMS values are computed in the following order:

1). RMS Voltage Calculation from Peak Voltage

V_RMS = V_peak-voltage X (1/ (√2)) = V_peak-voltage X 0.7071

2). RMS Voltage Calculation from Peak – Peak Voltage

V_RMS = V_peak-voltage X (1/ 2(√2)) = V_peak-peakX 0.3536

3). RMS Voltage Calculation from Average Voltage

V_RMS = V_averageX (∏/ (√2)) = V_average X 1.11

Calculator to calculate RMS Voltage

Equivalent of RMS Voltage

There are primarily two primary ways for calculating the RMS voltage value of a sine wave (or) other complex waveform. The methods are as follows:

1). RMS Voltage Graphical Method – This method is used to determine the RMS voltage of a time-varying non-sine wave. This may be accomplished simply pointing at the wave’s mid-ordinates.

2). RMS Voltage Analytical Method – This method uses mathematical calculations to compute the voltage of a wave.

1). RMS Voltage Graphical Method (Graphical Approach)

This method demonstrates the same method for calculating the RMS value for the positive & negative half of the wave.

As a result, this  describes how a positive cycle works. The value may be computed by taking into account a certain level of precision for each equally spaced moment throughout the waveform.

The positive half cycle is divided into ‘n’ equal sections known as middle ordinates. If there are many numbers of middle ordinates, then the result will be more accurate.

As a result, the breadth of each middle ordinate is n degrees, & the height is the instant value of the wave over the wave’s x-axis.

Every value in the wave’s middle ordinate is doubled & then added to the following value. The squared value of the RMS voltage is obtained using this method.

The resulting value is then divided by the entire number of middle ordinates, yielding the RMS voltage Mean value. As a result, the RMS voltage equation is

V_rms = √ [(v₁²+v₂²+v₃²+……+v_n²)]/ number of the middle ordinates

2). RMS Voltage Analytical Method (Analytical Approach)

This method only works with sine waves, which are simple to obtain the RMS voltage values for using a mathematical approach.

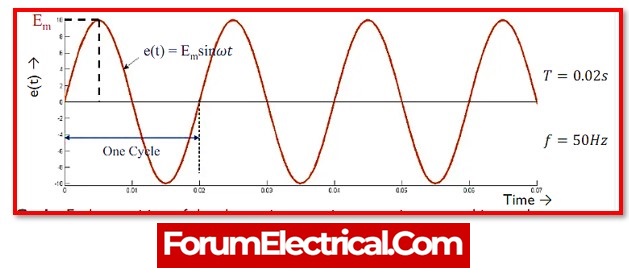
Assume a pure sinusoidal voltage waveform with a period of T specified as V_maxCos(ωt).

Where,

V_max = Maximum or Peak voltage waveform value

ω = Angular frequency

i.e.,ω = 2π/T

A periodic sine wave has a constant frequency and is denoted as

V_(t) = V_max x cos(ωt)

In this condition, the RMS value of the sine voltage V_(t) is used.

V_RMS = √(1/T ʃ^T₀V_max² x cos²(ωt))

When the integral limits are recognised between 0⁰ and 360⁰, then

V_RMS = √(1/T ʃ^T₀V_max² x cos²(ωt))

RMS voltage is the correct method to express the signal magnitude, current, & voltage values when correlating to AC voltages. The RMS value is not comparable to the median of all instant values. The percentage to the RMS voltage and peak voltage value is comparable to the proportion to the RMS current and peak current value.

Many multimeter instruments, whether ammeters or voltmeters, compute RMS values based on accurate (correct) sine waves. An “Accurate Multimeter” is required to measure the RMS value of the non-sine wave. The value determined by the RMS method for a sine wave has a comparable heating effect to that of a DC wave.

Function and calculator to calculate Peak Voltage are detailed.

Function and calculator to calculate Peak-Peak Voltage are detailed.