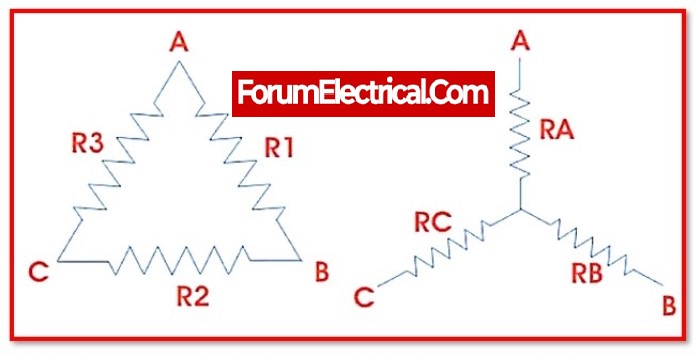
The Delta-Star transformation is a technique in electrical engineering that allows the impedance of a three-phase electrical circuit to be transformed from a “delta” configuration to a “star” (also known as “Y”) configuration, or vice versa. The delta configuration is a circuit in which the three phases are connected in a loop, with each phase connected to the other two phases. The star configuration is a circuit in which the three phases are connected to a common point, or “neutral” point.
The Delta-Star transformation allows the impedance of a three-phase circuit to be expressed in either the delta or the star configuration, depending on which is more convenient for a given analysis or design problem. The transformation is based on the following relationships:
- The impedance of a phase in a delta configuration is equal to the impedance of the corresponding phase in a star configuration divided by 3.
- The impedance of a phase in a star configuration is equal to the impedance of the corresponding phase in a delta configuration multiplied by 3.
The Delta-Star transformation is a useful tool for analyzing and designing three-phase electrical circuits, particularly when the circuit contains both delta-connected and star-connected elements. It allows engineers to use symmetry to simplify the analysis of the circuit, making it easier to understand its behavior and to design it effectively.
Delta Network:
Consider the delta network shown in the diagram:
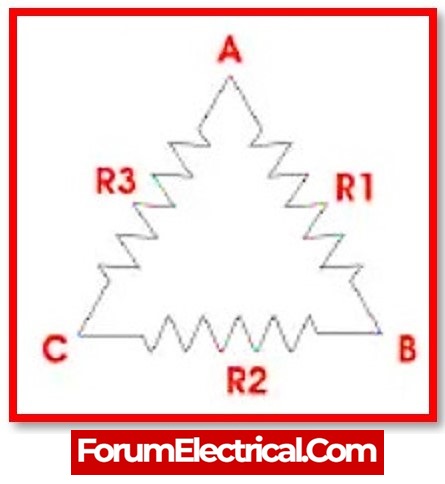
When the third terminal is left open, the following equations represent the equivalent resistance that exists between two terminals in a delta network.
RAB = (R1+R3) R2/R1+R2+R3
RBC = (R1+R2) R3/R1+R2+R3
RCA = (R2+R3) R1/R1+R2+R3
Star Network:
The corresponding star network to the above delta network is shown in the diagram below:
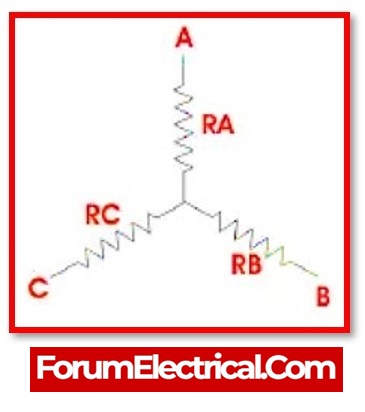
When the third terminal of a star network is maintained open, the following equations indicate the equivalent resistance between the two terminals.
RAB = RA+RB
RBC = RB+RC
RCA = RC+RA
Resistances of the Star Network in terms of Delta Network Resistances:
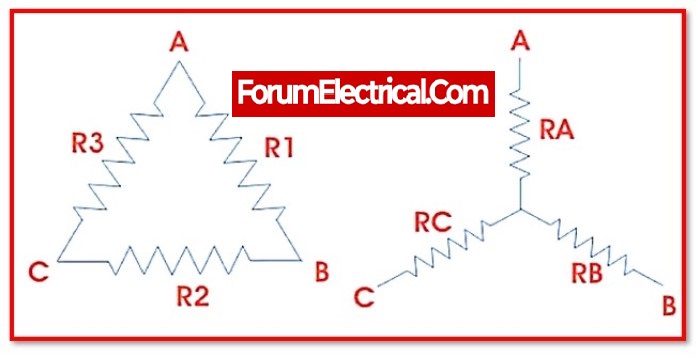
By equating the right-hand side terms of the previous equations for which the left-hand side terms are the same, will get the following equations.
Equation 1: RA+RB = (R1+R3) R2/R1+R2+R3
Equation 2: RB+RC = (R1+R2) R3/R1+R2+R3
Equation 3: RC+RA = (R2+R3) R1/R1+R2+R3
By combining the three equations above, will get
2(RA+RB+RC) = 2 (R1R2+R2R3+R3R1)/R1+R2+R3
Equation 4: RA+RB+RC = R1R2+R2R3+R3R1/R1+R2+R3
Equation 2 is subtracted from Equation 4,
RA = R1R2 / R1+R2+R3
Equation 3 is subtracted from Equation 4,
RB = R2R3 / R1+R2+R3
Equation 1 is subtracted from Equation 4,
RC = R3R1 / R1+R2+R3
Using the above equations, can calculate the resistances of the star network from the resistances of the delta network. In this manner, a delta network can be converted into a star network.
The Delta-Star transformation is only applicable to three-phase electrical circuits. It is not applicable to circuits with a different number of phases.