Nodal voltage analysis is a method used in electrical engineering to analyze and solve circuits using the concept of “nodal voltages.” It involves assigning voltage variables to nodes in the circuit and using Kirchhoff’s laws and Ohm’s law to solve for the unknown voltages.
To perform nodal voltage analysis, the circuit is first divided into a number of nodes, or “reference points.” The voltage at each node is then chosen as a variable and is typically denoted with the letter “V,” followed by a subscript indicating the node at which the voltage is measured.
Next, Kirchhoff’s laws and Ohm’s law are used to write a set of equations that describe the relationships between the nodal voltages and the currents in the circuit. Kirchhoff’s voltage law states that the sum of the voltage drops around a loop must equal the sum of the voltage sources in that loop. Kirchhoff’s current law states that the sum of the currents entering a node must equal the sum of the currents leaving that node. Ohm’s law states that the voltage drop across a resistor is equal to the resistance of the resistor multiplied by the current flowing through it.
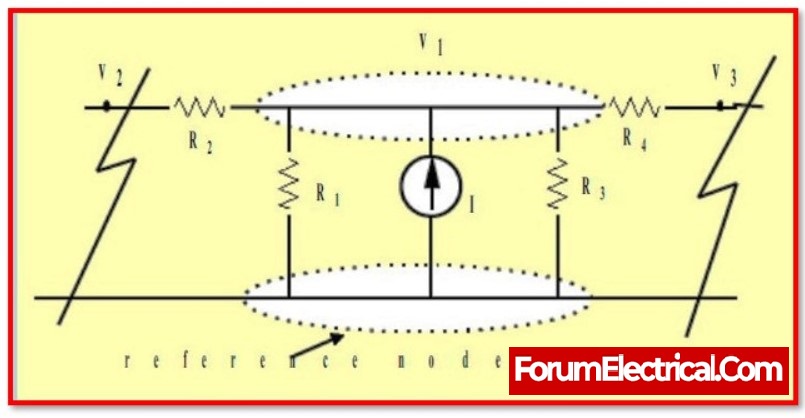
Consider the node voltages with respect to Ground in Nodal analysis. As a result, Nodal analysis is also known as the Node-voltage method.
Nodal Analysis Procedure:
When applying Nodal analysis to solve any electrical network or circuit, follow these steps.
Step 1: Determine the principal nodes and select one of them as the reference node. That reference node will be referred to as the Ground.
Step 2: Label the node voltages from all primary nodes except the reference node with respect to Ground.
Step 3: Create nodal equations for each of the primary nodes excluding the reference node. The nodal equation is determined by first applying KCL and then Ohm’s law.
Step 4: To obtain the node voltages, solve the nodal equations acquired in Step 3.
Using node voltages, can able to find the current flowing through any element and the voltage across any element in the provided network.

By solving the set of equations derived from Kirchhoff’s laws and Ohm’s law, the values of the nodal voltages can be determined. Once the nodal voltages are known, the currents in other parts of the circuit can be found by applying Kirchhoff’s laws and Ohm’s law again.
Nodal voltage analysis is a useful method for analyzing and solving circuits, particularly when the circuits contain dependent sources or when it is not possible to use other methods, such as mesh current analysis or loop analysis. It is a powerful tool that allows engineers to predict the behavior of complex circuits and to design them to meet specific performance requirements.
Type of Nodes in Nodal Analysis:
Non-Reference Node:
- A node with a fixed Node Voltage.
- e.g. Non Reference nodes are Nodes 1 and 2.
Reference Node:
- A node that serves as a point of reference for all other nodes.
- It’s also known as the Datum Node.
Reference Node Types:
Chassis Ground:
A reference node that acts as a common node for multiple circuits.

Earth Ground:
When earth potential is utilised as a reference in any circuit, this form of reference node is referred to as Earth Ground.
Nodal Analysis Characteristics:
- Kirchhoff’s Current Law is used to do Nodal Analysis (KCL).
- With ‘n’ nodes, there will be ‘n-1’ simultaneous equations to solve.
- The voltages of all the nodes can be found by solving ‘n-1’ equations.
- The number of non-reference nodes is equal to the number of Nodal equations can be obtained.









