Mesh current analysis is a method used in electrical engineering to analyze and solve circuits with multiple loops or “meshes.” It involves assigning currents to each loop in the circuit and using Kirchhoff’s laws and Ohm’s law to solve for the unknown currents.
To perform mesh current analysis, the circuit is first divided into a number of non-intersecting loops, or “meshes.” The direction of the current in each loop is then chosen and a variable is assigned to represent the current in that loop. The variables chosen for the currents are typically denoted with the letter “I,” followed by a subscript indicating the loop in which the current flows.
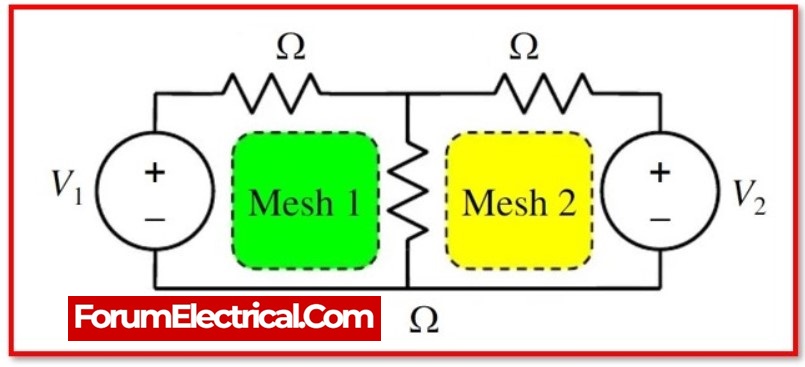
Next, Kirchhoff’s laws and Ohm’s law are used to write a set of equations that describe the relationships between the currents and the voltage drops in the circuit. Kirchhoff’s voltage law states that the sum of the voltage drops around a loop must equal the sum of the voltage sources in that loop. Kirchhoff’s current law states that the sum of the currents entering a node (a point where three or more branches meet) must equal the sum of the currents leaving that node. Ohm’s law states that the voltage drop across a resistor is equal to the resistance of the resistor multiplied by the current flowing through it.
By solving the set of equations derived from Kirchhoff’s laws and Ohm’s law, the values of the mesh currents can be determined. Once the mesh currents are known, the currents in other parts of the circuit can be found by applying Kirchhoff’s laws and Ohm’s law again.
Mesh current analysis is a useful method for analyzing and solving circuits with multiple loops, particularly when the circuits contain dependent sources or when it is not possible to use other methods, such as nodal analysis or loop analysis. It is a powerful tool that allows engineers to predict the behavior of complex circuits and to design them to meet specific performance requirements.
In mesh analysis, how do you calculate current?
The Mesh Current Method consists of the following steps:
1. Determine the meshes.
2. Assign a current variable to every mesh in either a clockwise or anticlockwise direction.
3. Around each mesh, write Kirchhoff’s Voltage Law.
4. For all loop currents, solve the resulting system of equations.
Why is mesh analysis used?
Mesh analysis is an effective and general method for determining unknown currents and voltages in any circuit. The problem is solved after the loop currents are determined, because any current in the circuit can then be calculated using the loop currents.
What is branch in mesh analysis?
A branch is a path that connects two nodes that includes a circuit element. When a branch belongs to only one mesh, the branch current equals the mesh current.
If two meshes share a branch, the branch current is equal to the sum (or difference) of the two mesh currents while they are in the same (or opposite) direction.
What is Loop?
Loop refers to any closed path in a circuit that does not pass through the same node more than once.









