NORTON’S THEOREM

Norton’s Theorem is a principle in electrical engineering that allows the complex impedance of an electric circuit to be reduced to a single equivalent impedance. It states that any linear, two-terminal electrical network can be represented by an equivalent circuit consisting of a single current source in parallel with a single impedance. The current of the source is the short-circuit current of the network, and the impedance is the impedance seen looking into the circuit with the current source removed and the terminals open-circuited. Norton’s Theorem is named after the American engineer E. L. Norton, who first proposed it in the early 20th century.

STATEMENT OF NORTON’S THEOREM:

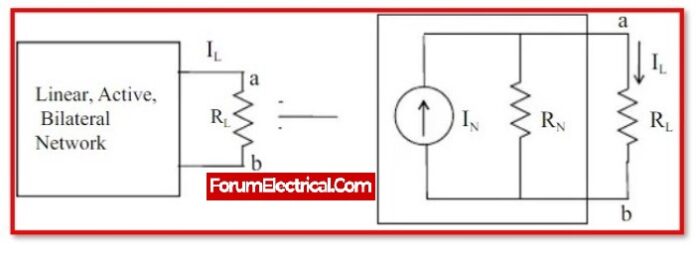
Any linear, active, bidirectional dc network with a number of voltage sources and/or current sources with resistances can be substituted by a simple equivalent circuit with a single current source (I_N) in parallel with a single resistance (R_N).

Where,

(I_N) is the Norton’s equivalent current across terminals a-b.

(R_N) is the Norton’s equivalent resistance across terminals a-b.

Similar to Thevenin’s theorem, except that the voltage source is gradually replaced by a current source

Find the Thevenin equivalent circuit first, then convert it to an equivalent current source.

The Norton equivalent resistance:

R_N =R_TH

The Norton equivalent current:

I_N = V_TH/R_TH

I_N denotes the current flowing in the short circuit connected across the terminals where the Norton equivalent circuit is required.

The Norton equivalent circuit is a useful tool for analyzing and designing electrical circuits because it allows the circuit to be represented by a single, simplified model. This makes it much easier to understand the behavior of the circuit and to calculate its response to different input signals.

To determine the Norton equivalent of a circuit, the following steps can be followed:

• Remove all independent sources from the circuit and open the terminals.
• Determine the impedance looking into the terminals with the sources removed. This is the Norton impedance.
• Restore the sources to the circuit and determine the short-circuit current at the terminals. This is the Norton current.
• The Norton equivalent circuit is a current source with a value equal to the Norton current in parallel with an impedance equal to the Norton impedance.
• Norton’s Theorem is only applicable to linear, two-terminal networks. It is not applicable to nonlinear circuits or circuits with more than two terminals.