Star-Delta transformation Theorem

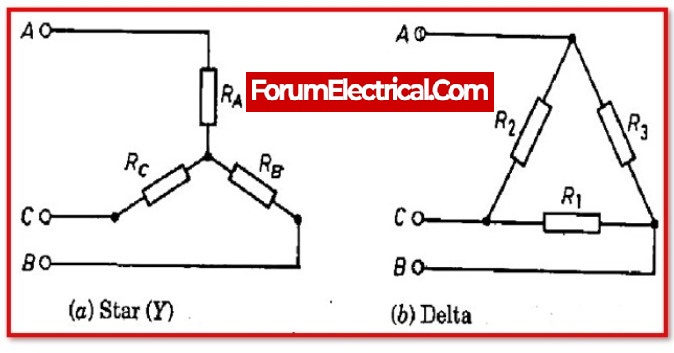
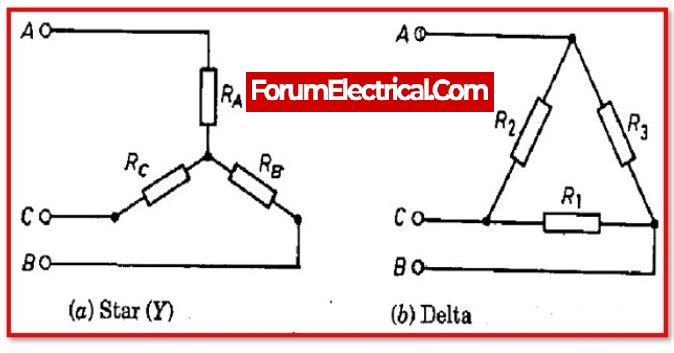
The Star-Delta transformation is a technique in electrical engineering that allows the impedance of a three-phase electrical circuit to be transformed from a “delta” configuration to a “star” (also known as “Y”) configuration, or vice versa. The delta configuration is a circuit in which the three phases are connected in a loop, with each phase connected to the other two phases. The star configuration is a circuit in which the three phases are connected to a common point, or “neutral” point.

The Star-Delta transformation allows the impedance of a three-phase circuit to be expressed in either the delta or the star configuration, depending on which is more convenient for a given analysis or design problem. The transformation is based on the following relationships:

• The impedance of a phase in a delta configuration is equal to the impedance of the corresponding phase in a star configuration divided by 3.
• The impedance of a phase in a star configuration is equal to the impedance of the corresponding phase in a delta configuration multiplied by 3.

The Star-Delta transformation is a useful tool for analyzing and designing three-phase electrical circuits, particularly when the circuit contains both delta-connected and star-connected elements. It allows engineers to use symmetry to simplify the analysis of the circuit, making it easier to understand its behavior and to design it effectively.

The Star-Delta transformation is only applicable to three-phase electrical circuits. It is not applicable to circuits with a different number of phases.

R_A=R₁R₂/(R₁+R₂+R₃)  ——— Equation 1

R_B=R₂R₃/(R₁+R₂+R₃)  ——— Equation 2

R_C=R₃R₁/(R₁+R₂+R₃)  ——— Equation 3

Multiply and then add each set of two equations.

R_AR_B+R_BR_C+R_CR_A=R₁R₂²R₃+R₂R₃²R₁+R₃R₁²R₂/(R₁+R₂+R₃)²

R_AR_B+R_BR_C+R_CR_A= R₁R₂R₃ (R₁+R₂+R₃)/(R₁+R₂+R₃)²

R_AR_B+R_BR_C+R_CR_A = (R₁+R₂+R₃)/(R₁+R₂+R₃) ———- Equation 4

Divide Equation 4 by Equation 2 and get

R₁=R_C+R_A+(R_C/R_AR_B)

Divide Equation 4 by Equation 3 and get

R₂=R_A+R_B+(R_A/R_BR_C)

Divide Equation 4 by Equation 1 and get

R₃=R_B+R_C+(R_B/R_CR_A)

The resistances of the delta network can be found using the above relations. In this technique, a star network can be converted into a delta network.